Fig. 1: Cart and pendulum

Optimization problems such as inverse dynamics and parameter identification problems are solved in ProtoFrame® by using the adjoint method. Although, the equations and matrices included show a complicated structure, the additional effort when combining the standard forward solver to the adjoint backward solver, is kept in limits.
The adjoint method shows an efficient way to incorporate inverse dynamics to engineering multibody applications, such as the automated matching of real and virtual prototypes. Therefore, we introduce a performance measure in the form [math]!J=\int_{0}^{T} h(x,u,t)\mathrm{d}t\rightarrow \min[/math] which incorporates the mean deviation between the simulated and measured system outputs. Minimizing this performance measure leads to the optimal set of parameters. By using the gradient out of inverse dynamics the optimization can be done more efficient.
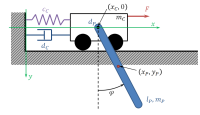
A simple academic example of a rigidly modeled cart pendulum presents the application of the adjoint method for parameter identification in multibody dynamics, see Fig. 1. For finding the damping parameters d_c and d_P, measured data of the cart position and the pendulum angle are used.
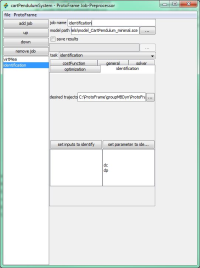
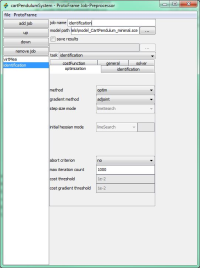
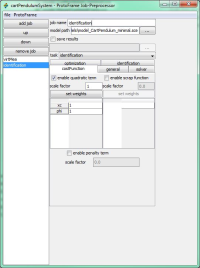
The following illustrations show the parameter identification mentioned above using the Protoframe® GUI.

Fig. 2: Protoframe GUI/preProcessor: set up identification task

Fig. 3: Protoframe GUI/preProcessor: set up optimization task for identification

Fig. 4: Protoframe GUI/preProcessor: set up cost function for identification

Fig. 5: Protoframe GUI/postProcessor: course of the cost function J as a function of the number of iteration steps

Fig. 6: Protoframe GUI/postProcessor: course of the estimated parameters as a function of the number of iteration steps